Такое понятие как волатильность слышал, наверное, каждый инвестор. Во время всем известного краха фондовой биржи в октябре 1987 года Индекс Доу-Джонса за один день упал на 512 пунктов (25%). Это привело к лавинообразным движениям цен на всех других биржах, и как следствие, к росту волатильности на биржах всего мира. Хотя и считается, что наибольший рост волатильности связан с большим падением цен, истинная причина не всегда кроется в этом. Фондовые рынки, охваченные паникой инвесторов, зачастую устанавливают свои правила игры, заставляя инвесторов менять тактику. Хотя многие имеют представление о том, что такое волатильность, мало кто знает, как она измеряется, а многие просто путают ее с направлением. Что же такое волатильность  и чем это может нам грозить?

Волатильность или изменчивость (volatility) это статистический и финансовый показатель, характеризующий изменчивость цены актива. Волатильность является одним из важнейших параметров в управлении финансовыми рисками. Именно она представляет собой меру риска владения финансовым инструментом на определенном отрезке времени. Волатильность предназначена измерять степень колебания актива, а не тенденции. Чем выше волатильность, тем выше риск. Но что такое финансовый риск? Давайте для начала разберемся в этом.

Когда мы говорим о финансовом риске, связанным с инвестициями и характеризуемым волатильностью, мы подразумеваем рыночный риск. Рыночный риск (market risk) – это возможность несоответствия характеристик экономического состояния объекта значениям, ожидаемым лицами, принимающими решения под действием рыночных факторов. Вот так мудрено. На самом деле, те, кто хоть раз покупал акцию или облигацию, прекрасно знает, что рыночный риск – это вероятность того, что «все пойдет, не так хорошо, как ты планировал».

Рыночные риски – одна из трех, часто выделяемых на практике основных групп экономических рисков, включающих так же кредитные и операционные риски. Рыночные риски связаны с неопределенностью колебаний рыночной конъюнктуры – ценовыми и курсовыми (валютными) рисками, процентным риском, ликвидностью и т. п. – и чувствительностью к этим рискам активов. Не только прямые ценовые факторы являются источниками рыночных рисков. Например, корреляция* между доходностью различных инструментов не является прямым ценовым фактором, но косвенно влияет на ценовые характеристики портфеля, содержащего эти инструменты.

* при объединении в портфеле двух или более рискованных активов, важную роль в определении волатильности портфеля играет корреляция (correlation) между их доходностями.

Корреляция – это статистическая взаимосвязь двух или нескольких случайных величин.

Приведу пример далекий от финансовых рынков. Например, измеряем рост и вес человека, каждое измерение представлено точкой в двумерном пространстве:

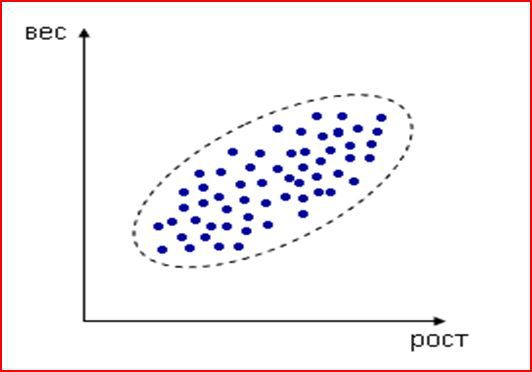
Несмотря на то, что величины носят случайный характер, в общем наблюдается некоторая зависимость — величины коррелируют.

В данном случае это положительная корреляция (при увеличении одного параметра второй тоже увеличивается). Возможны также такие случаи:

Отрицательная корреляция

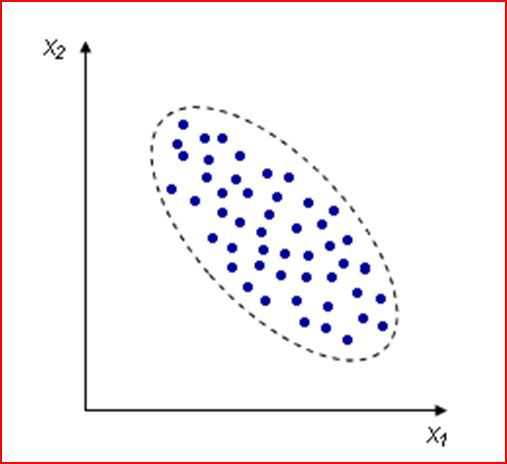
Корреляция отсутствует

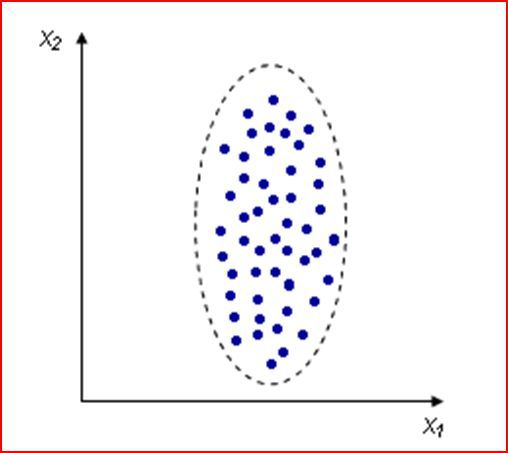
Взаимосвязь между переменными необходимо охарактеризовать численно, чтобы, например, различать такие случаи: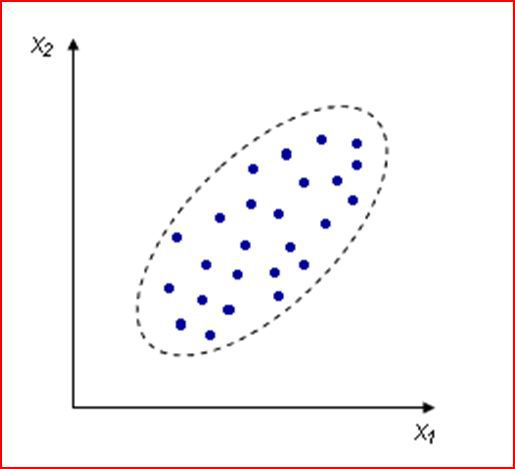

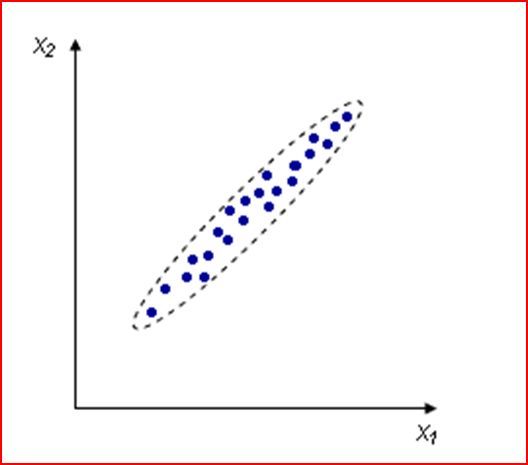
Для этого вводится коэффициент корреляции. Коэффициент корреляции всегда лежит в интервале от -1 до +1.

Классификация рыночных рисков нужна, так как она позволяет структурировать проблеммы и влияет на анализ ситуации. Можно выделить наиболее широкоупотребляемую классификацию рыночных рисков по сегментам рынка, в том числе:

• процентный риск (interest rate risk);
• валютный риск (exchange rate risk);
• ценовой риск рынка акций, или фондовый риск (equity risk);
• ценовой риск товарных рынков, или товарный риск (derivative risk).

Два важных аспекта характеризуют рыночный риск : во-первых, волатильность или (изменчивость) доходности финансового актива, и, во-вторых, чувствительность (exposure) цены активов к изменению волатильности. Это очень важно понимать, так как мы не можем влиять на волатильность, но мы можем изменить чувствительность своего портфеля к изменениям волатильности! То есть рыночный риск может быть частично нивелирован, например, с помощью производных инструментов.

И еще немного о чувствительности, что бы было понятно, о чем идет речь. Измерители чувтвительности к изминению волатильности используются под различными обозначениями. На рынке инструментов с фиксированной доходностью чувствительность к движению процентных ставок измеряется дюрацией. На рынке акций чувствительность к фактору рынка в целом  (например, к изменению величины фондового индекса) называется систематическим риском или коэффициентом бета. На рынке производных инструментов чувствительность к изменению цены базового актива измеряется коэффициентом дельта. Скорость изменения дюрации к изменению процентных ставок в свою очередь характеризуется выпуклостью. А изменчивость дельты при изменении цены базового актива – коэффициентом гамма.

При измерении рыночного риска в качестве случайной переменной обычно берут не цену актива, а его доходность (return) финансового актива. Каким образом определяется доходность актива?

Пусть период равен одному месяцу. Арифметическая или дискретная доходность актива за месяц определяется как прирост стоимости актива за этот период, плюс возможные промежуточные выплаты за этот период (купоны или дивиденды):

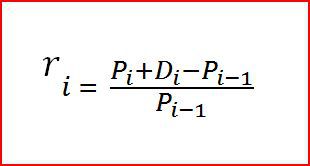
Где  Pi — цена актива на конец исследуемого периода;

Pi — 1 – цена актива на начало исследуемого периода;

Di— выплаты в исследуемом периоде.

При расчете волатильности используют такое понятие, как «ожидаемая доходность». На практике определение доходности обычно оценивается по историческим данным, предполагая, что наблюдения идентичны и независимо распределены. В этом случае, если N – число наблюдений, то ожидаемую доходность можно принять как простую среднюю:

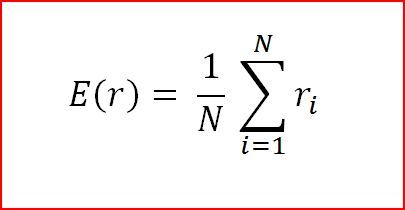
И вот мы почти на финишной прямой расчета волатильности.

Какая информация обычно имеется в наличие при работе с фактическими данными? В общем случае мы знаем как меняется цена на определенном интервале и, следовательно, можем расчитать доходности и ожидаемую доходность, как среднее значение. Каким же образом мы можем расчитать волатильность? Наивное решение состоит в том, что бы рассматривать все прошлые наблюдения как реализацию случайных величин. Тогда каждую доходность рассматривают как равновзвешенную. На самом деле, на практике так обычно и делается, чтобы избежать дополнительной сложности, а так же потому, что наиболее распространенные программные средства не дают удобных инструментов для проведения соответствующего анализа. Поэтому наблюдаемые систематические ошибки просто игнорируются. Исходя из известных нам данных, волатильность расчитывается следующим образом:

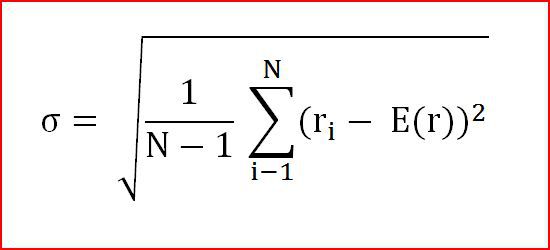
Она измеряет риск актива как степень разброса значений доходности вокруг ожидаемой доходности.

Что вообще это нам дает? Надо отметить, что величина σ имеет непосредственное отношение к нормальному закону распределения случайной величины. Принято считать, что именно этому закону в большинстве случаев подчиняется случайное распределение двух независимых величин. Но необходимо заметить, что нормальное распределение в лучшем случае является разумным приближением распределения доходности актива, но не совершенной моделью. Это неточная модель реальности, но за неимением лучшего, именно ее чаще всего и используют.

Параметр σ характеризует не положение, а самую форму кривой распределения. Это есть характеристика рассеивания. Поясню на примере.

Закон нормального распределения случайных величин или закон Гаусса графически выглядит следующим образом: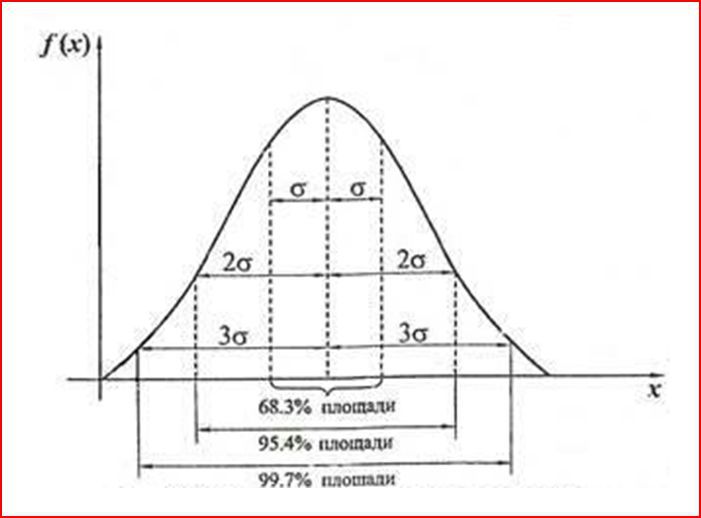

Вот и σ появилась. Согласно закону нормального распределения случайных величин, отклонение будущих значений доходности (в нашем случае) с вероятностью 68,3% будут находиться в пределах  σ от ожидаемой доходности; с вероятностью 95,4% — в пределах 2σ и с вероятностью 99,7% — в пределах 3σ от ожидаемой доходности. Данная величина σ, или стандартное отклонение – и есть искомая волатильность. Стандартное отклонение или волатильность измеряется в процентах, то есть в тех же единицах, что и доходность.

Пример:

Давайте попробуем определить стандартное отклонение доходности акции, если ее доходность за первый год составила 20%, за второй год —  35%, за третий год – минус 2%, за четвертый год – 15%, за пятый – 10%.

Определим среднюю доходность акции (ожидаемую доходность):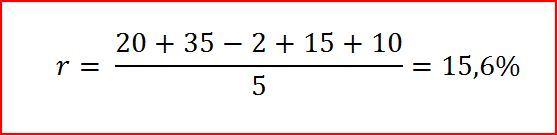

Определим стандартное отклонение или волатильность акции: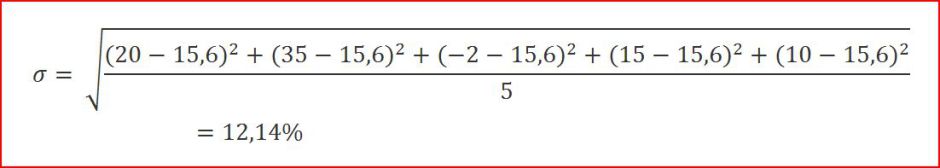

А теперь посмотрим на график. С вероятностью 68,3% доходность нашей акции будет находиться в интервале от 3,46% годовых до 27,74% годовых. С вероятностью 95,4% — в интервале от (-8,68%) до 39,88 %. И с вероятностью 99,7% (очень высокая вероятность!!!) – в интервале от (– 20,82%) до 52,02%. Остается еще вероятность 0,3%, что акция принесет нам или гораздо больший доход или гораздо больший убыток. Наверно, именно в этих 0,3% парят «черные лебеди» Нассима Талеба.*

*«Чёрный лебедь» — теория, рассматривающая труднопрогнозируемые и редкие события, которые имеют значительные последствия. Автором теории является Нассим Николас Талеб, который в своей книге «Черный лебедь. Под знаком непредсказуемости» ввел термин «событие типа «черный лебедь» (The Black Swan, TBS).

Согласно критериям, предложенным автором теории событие является неожиданным, событие производит значительные последствия, после наступления, в ретроспективе, событие имеет рационалистическое объяснение, как если бы событие было ожидаемым.

С точки зрения автора практически все значимые научные открытия, исторические и политические события, достижения искусств и культуры – это Черные лебеди. Примерами Черных лебедей является развитие и внедрение Интернета, Первая мировая война, развал СССР, 11 сентября или тот же Brexit. Талеб также отмечает, что человечество не способно успешно прогнозировать свое будущее, а уверенность в своих знаниях опережает сами знания и порождает феномен «сверхуверенности».

Рассчитывая стандартное отклонение в данном примере, мы оперировали временным интервалом равным году. На практике часто возникает задача определения стандартного отклонения для других временных интервалов.

Если мы рассчитали стандартное отклонение за год, то для определения его за один день надо стандартное отклонение в расчете на год разделить на корень квадратный из количества торговых дней в году. В году насчитывается порядка 252 торговых дней. Поэтому стандартное отклонение доходности актива за день можно рассчитать следующим образом:

Или для нашей акции:

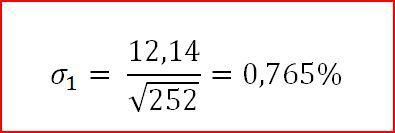
Если нам нужно определить стандартное отклонение за некоторый период времени на основе годичного стандартного отклонения, то в общем виде формула будет иметь следующий вид:

На практике приемлемый результат получается, если рассчитывать стандартное отклонение для более длительных периодов на основе более коротких, используя периоды времени до 10 дней.

Интервалы времени, за которые рассчитывается стандартное отклонение, могут быть самыми разными: часы, дни, недели, месяцы, годы. Существует много способов проведения выборки для вычисления волатильности. Используем ли мы дневные, недельные или месячные цены? Какой берем временной интервал? Точность всех используемых статистических данных является необходимым условием выборки. Использовать 200 элементов выборки лучше, чем 50. Но насколько недель назад – на 200 или на 50 – мы должны вернуться в прошлое для определения волатильности? Если отсчитать 200 недель, то мы можем включить в расчет данные, которые уже настолько устарели, что скорее увеличат, нежели уменьшат вероятность ошибки. Опыт подсказывает, что волатильность постоянно изменяется, поэтому лучше изучать не очень большой временной интервал.

Дисперсию как меру риска ввел в теорию портфеля ценных бумаг основоположник современной теории портфеля  Г. Марковиц.* Определенным недостатком данной меры риска является то, что она одинаково учитывает отклонения в доходности активов от его средней доходности как в сторону увеличения, так и снижения. В тоже время инвестора в плане оценки риска волнует именно снижение доходности актива. Для инвестора, купившего актив, рост доходности актива по сути не является риском.

*Гарри Макс Марковиц (24.08.1927 г.) – американский экономист (Калифорнийский университет в Сан-Диего).

Гарри Марковиц окончил Чикагский университет, степень доктора получил там же; основоположник современной портфельной теории. Известен пионерской работой, в которой предложил новый подход к исследованию эффектов риска распределения инвестиций, корреляции и диверсификации ожидаемых инвестиционных доходов. Марковиц лауреат Нобелевской премии 1990 года «за работы по теории финансовой экономике».

На практике волатильность может определяться не только путем расчета непосредственно по статистике цен актива, но и исходя из моделей ценообразования производных инструментов. Если обобщить, то существует три типа волатильности:

Историческая – фактическая волатильность цены актива в течение определенного исторического периода времени;

Ожидаемая – рыночная оценка волатильности на будущее;

Ожидаемая историческая – «летопись прогнозов» ожидаемой волатильности.

Как считать историческую волатильность мы поговорили выше.

Ожидаемую волатильность можно определить исходя из рыночной стоимости опционов на интересующий нас актив. При этом подразумевается, что если модели ценообразования опционов в качестве одной из переменных предполагают использование волатильности базового актива, то можно решить обратную задачу и вычислить по фактическим котировкам опционов предполагаемую (implied) волатильность, которая отражает текущие ожидания участников рынка (подробнее можно посмотреть в статье «Опционы 2»).

В реальности опционов с разными параметрами  на один и тот же базовый актив может быть множество, и ожидаемая волатильность по каждому из них может не совпадать, поэтому для прогноза применяют различные модели усреднения этих данных.

Именно таким образом рассчитывается один из самых популярных индексов волатильности —  CBOE Volatility Index (VIX). Ожидаемая волатильность рассчитывается с использование корзины пут и колл опционов out-of-the-money (вне денег) на Индекс S&P500. Чикагская биржа опционов (CBOE) вычисляет индексы волатильности для ряда различных индексов, в том числе золото,  нефть, валюта, промышленные индексы Dow Industrials, S & P 500 и Nasdaq 100.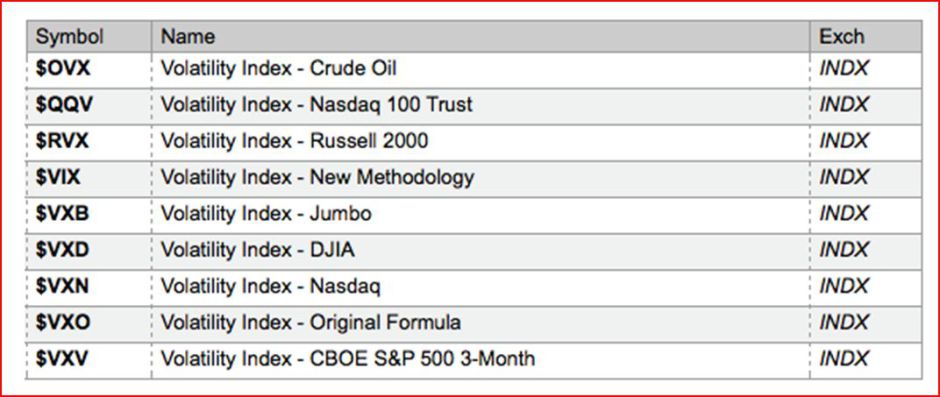

С 2013 года на Московской бирже также рассчитывается индекс волатильности  RVI. Методика его расчета также базируется на корзине опционов. Все об этом индексе можно посмотреть здесь: http://moex.com/ru/index/RVI/info/.

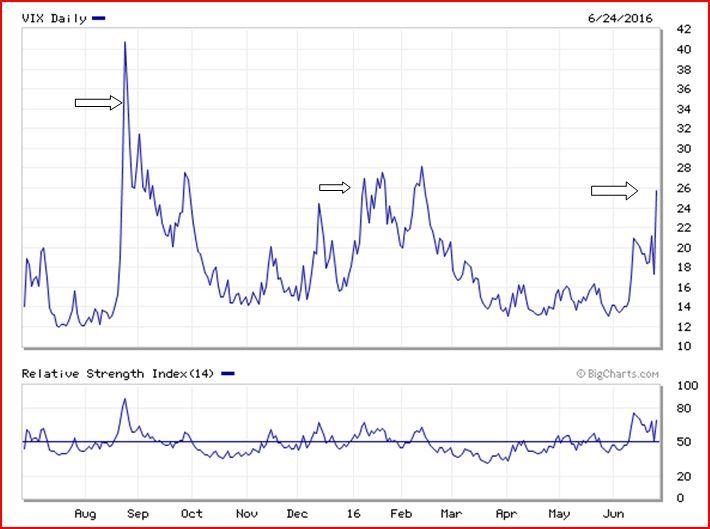
Обычно индекс волатильности имеет обратную зависимость от движений актива на рынке. Если цены падают, то индекс волатильности растет, и если цены растут или остаются в узком диапазоне, то индекс волатильности снижается. Надо отметить, что скорость роста индекса при падении рынка выше, чем его падение при росте рынка на такую же величину. Причина в том, что бычий рынок рассматривается участниками как менее рискованный, в отличие от падающего. То есть неравнозначное восприятия роста рынка и его падения с точки зрения риска, приводит к «перекосу» движения индекса волатильности. Именно из-за этого перекоса для индекса волатильности при падении рынка характерны очень сильные «всплески». Скорее всего, именно из-за них его также называют «индексом страха». В качестве примера график VIX. Последняя стрелочка – BREXIT.

Многие аналитики считают индекс волатильности синхронным индикатором. Но он может служить индикатором тренда. Большинство участников рынка  больше обращают внимание на выход значений  индекса волатильности за определенные пределы. Подъем или падение за пределы определенных значений могут сигнализировать о скором развороте рынка. Практика подтверждает то, что называется «возвращением к средней величине» волатильности. Проще говоря, если определенный ценовой ряд начинает демонстрировать высокую волатильность, то она, в конце концов, понизится. Точно также, если ряд начинает демонстрировать чрезвычайно низкую волатильность, она в конечном итоге поднимется. Теория предполагает существование некоторого долгосрочного уровня средней волатильности. Ее суть, безусловно, заключается в определении высоких и низких значений волатильности.

В качестве примера, я нашла достаточно старый, но весьма наглядный график для VIX (речь идет о 2008 годе).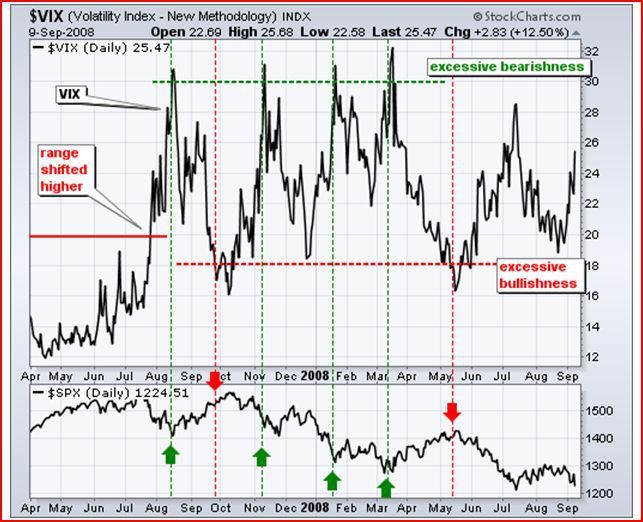

Как видно на графике, индекс волатильности в тот период не опускался ниже 15 (хотя в предыдущие годы, уровнем, сигнализирующем о «перекупленности» рынка, были значения индекса в районе 10-15). Уровнями, сигнализирующими о чрезмерной «перепроданности» рынка, принято считать 30-35. Удинственно, необходимо помнить, что эти уровни могут смещаться. Всегда необходимо ориентироваться на предшествующую историческую волатильность.

Конечно, это не идеальный источник информации, но, надо признать, достаточно эффективный в прогнозировании разворотов рынка, особенно, в области, так называемых «шипов» волатильности. И прежде, чем бросаться распродавать активы при значении волатильности ниже 15, обратите внимание, что низкая волатильность может длиться месяцами, и все это время рынок будет продолжать расти.

Это очень хорошо видно на следующем графике. Конечно, можно торговать «коротко», ловя краткосрочные всплески, но факт остается фактом, весь 2005, 2006 и 2007 годы волатильность продолжала падать, а рынок расти и расти.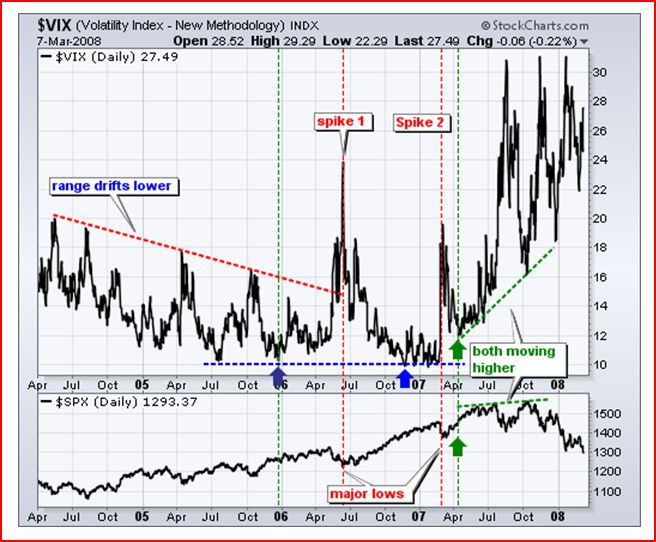

Индекс волатильности это все-таки больше индикатор настроения рынка. Лучше всего он идентифицирует крайности.

К сожалению, невозможно вычислить точное значение волатильности. Как и многое другое в финансовом деле, все вычисления, как бы они не были сделаны, всегда будут временными. Поэтому не стоит ожидать, что волатильность, рассчитанная в прошлом, — это удачный прогноз будущей волатильности.

Изучение волатильности может помочь не только взглянуть на рынок несколько под другим углом, но и сделать ваш портфель менее чувствительным к рыночной волатильности. Кроме этого, на рынке существуют торговые стратегии, основанные на изменении волатильности базового актива, а не его цены.

К сожалению, инвесторы очень часто осознают слово «риск» только получив выписку по счету или после того, как произошла потеря. Надеюсь, эта статья немного поможет приблизиться к понимаю рыночных рисков и к изучению методов их уменьшения.

Источник: http://cfocafe.co/index-straha/

 478 всего,  2 за сутки